On page 30 of Kimberley Elam’s book, "Geometry of Design: Studies in Proportion and Composition", she portrays a Golden Triangle inscribed in a Golden Ellipse inscribed in a Golden Rectangle.  I wanted to see how elegant the relationship between the triangle lengths and the other two might be, so I put pencil to paper.  After quite some while I arrived at a result which was neither elegant nor trivial, but as it took some effort I will present it here.

Given a Golden Rectangle of length f and height 1, the inscribed ellipse would follow the equation:

y = ½Ö[1 + 2x2(Ö5 – 3)]



The Golden Triangle, as depicted above, would set horizontally, symmetric to and bisected by the x-axis, touching the Golden Rectangle only at the leftmost point of the x-axis.  I calculated that the line passing through the left tangent of the ellipse to the superscribed Golden Rectangle such that the angle it made with the x-axis would be 18° to result in a Golden Triangle would be:

y = (Ö10/20){Ö(5 - Ö5) + 2xÖ[2(5 - 2Ö5)]}

Setting these two equations equivalent and solving for x gave the point (1/44)(5Ö5 + 9), with y = ±(1/11) Ö(25 - 2Ö5).  Armed with this point, we can compute the three distances of interest in the inscribed Golden Triangle: the base, the length of each leg of the isosceles triangle, and the height.  They are as follows:

Base = (2/11)Ö(25 - 2Ö5)                                                (2.1)
Leg = (1/11)Ö[2(65 + 19Ö5)]                                         (2.2)
Height = (1/11)(4Ö5 + 5)                                                   (2.3)




As the result was not elegant, I wondered about the OTHER Golden Triangle one can inscribe in the Golden Ellipse, the one set symmetric to and bisected by the y-axis, touching the superscribed Golden Rectangle only at the uppermost point of the y-axis, shown above.  The line passing down and to the right from the y-axis at this point making an angle of 18° with the y-axis would be:

y = -xÖ(5 + 2Ö5) + ½

The Golden Ellipse equation would be as above.  Setting the two equivalent and solving for x gives the position (1/62)Ö[2(145 + 19Ö5)].  Finding the corresponding y gives the three distances thus:

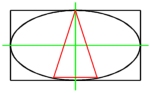
Base = (1/31)Ö[2(145 + 19Ö5)]                                         (2.4)
Leg = (1/31)Ö[2(265 + 101Ö5)]                                       (2.5)
Height = (1/62)(11Ö5 + 35)                                                 (2.6)

These two Golden Triangles are of course similar and proportional to each other, base to base, height to height, and therefore the ratio between those two sets is identical.  And of course the ratios between the base and leg of each is f.

Back to My Contributions page